1.GERAK PADA KATROL

Sistem benda
Sistem benda adalah gabungan beberapa benda yang mengalami gerak secara bersama-sama. Pada sistem benda pada materi ini dapat merupakan gabungan
gerak translasi dan rotasi.

Contohnya adalah sistem katrol dengan massa tidak diabaikan.

Contoh 1 :

Balok A 2 kg berada di atas meja licin dihubungkan tali dengan balok B 3 kg melalui katrol sehingga dapat menggantung seperti pada Gambar (a).
Jika massa katrol sebesar 2 kg dan jari-jari 10 cm maka tentukan :
a. percepatan benda A dan B,
b. percepatan sudut katrol,
c. tegangan tali TA dan TB!
Penyelesaian
mA = 2 kg
mB = 3 kg → wB = 30 N
mk = 2 kg → k =
a. Percepatan balok A dan B
Balok A dan B akan bergerak lurus dan katrol berotasi sehingga dapat ditentukan percepatannya dengan bantuan gambar gaya-gaya seperti pada Gambar (b).
Balok A : translasi
ΣF = m a
TA = mA a = 2 a ………………………………
a) Balok B : translasi
ΣF = m a
30 − TB = 3a
TB = 30 − 3a …………………………………
b) Katrol : berotasi
Στ = I α
(TB − TA) R = k mk R2 .
TB − TA = . 2 . a
Substitusi TA dan TB dapat diperoleh:
(30 − 3a) − (2a) = a
30 = 6a → a = 5 m/s2

b. Percepatan sudut katrol sebesar:
α = a / R = 5 / 0,1 = 50 rad/s²
c. Tegangan talinya:
TA = 2a = 2 . 5 = 10 N
TB = 30 − 3a = 30 − 3 . 5 = 15 N

Contoh 2, menghitung percepatan benda yang terhubung pada katrol

Sebuah silinder pejal berjari-jari 15 cm dan bermassa 2 kg dijadikan katrol untuk sebuah sumur, seperti tampak pada gambar. Batang yang dijadikan poros memiliki permukaan licin sempurna. Seutas tali yang massanya dapat diabaikan, digulung pada silinder. Kemudian, sebuah ember bermassa 1 kg diikatkan pada ujung tali. Tentukan percepatan ember saat jatuh ke dalam sumur.

Jawab

Diketahui: R = 15 cm, massa katrol silinder M = 2 kg, dan massa ember m = 1 kg.

Rotasi pada katrol silinder:
Berdasarkan persamaan momen gaya didapatkan
τ = Iα
RT = Ia/R
T = (I.a)/R² …. (a)

Translasi pada ember:
Berdasarkan Hukum Newton didapatkan

ƩF = m.a

mg – T = ma …. (b)

Dengan menggabungkan Persamaan (a) dan Persamaan (b), diperoleh hubungan.

Selanjutnya, substitusikan harga I = ½ M R2 pada Persamaan (c) sehingga diperoleh

dengan m adalah massa ember dan M adalah massa katrol silinder.

2.GERAK MENGGELINDING

Bola yang menggelinding di atas bidang akan mengalami dua gerakan sekaligus, yaitu rotasi terhadap sumbu bola dan translasi bidang yang dilalui. Oleh karena itu, benda yang melakukan gerak menggelinding memiliki persamaan rotasi dan persamaan translasi. Besarnya energi kinetik yang dimiliki benda mengelinding adalah jumlah energi kinetik rotasi dan energi kinetik translasi. Anda disini akan mempelajari bola mengelinding pada bidang datar dan bidang miring

1. Menggelinding pada Bidang Datar

Perhatikan Gambar 6.8! Sebuah silinder pejal bermassa m dan berjari-jari R menggelinding sepanjang bidang datar horizontal. Pada silinder diberikan gaya sebesar F. Berapakah percepatan silinder tersebut jika silider menggelinding tanpa selip? Jika silinder bergulir tanpa selip, maka silinder tersebut bergerak secara translasi dan rotasi. Pada kedua macam gerak tersebut berlaku persamaan-persamaan berikut.

• Untuk gerak translasi berlaku persamaan
F – f = m a dan N – m g = 0
Untuk gerak rotasi berlaku persamaan
τ= I x α

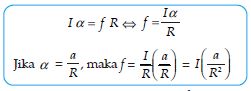
Karena silinder bergulir tanpa selip, maka harus ada gaya gesekan.
Besarnya gaya gesekan pada sistem ini adalah sebagai berikutJika disubstitusikan ke dalam persamaan F – f = m a, maka persamaanya

menjadi seperti berikut

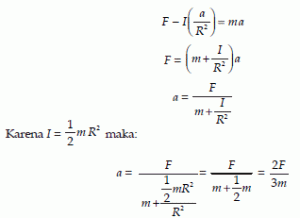
Contoh: Sebuah bola pejal bermassa 10 kg berjari-jari 70 cm menggelinding di atas bidang datar karena dikenai gaya 14 N. Tentukan momen inersia,percepatan tangensial tepi bola, percepatan sudut bola, gaya gesekan antara bola dan bidang datar, serta besarnya torsi yang memutar bola!

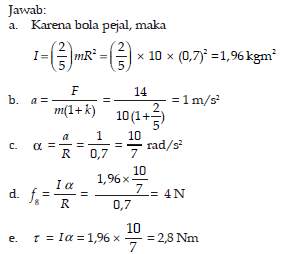
2. Menggelinding pada Bidang Miring

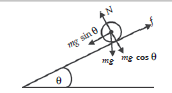
Gerak translasi diperoleh dengan mengasumsikan semua gaya luar bekerja di pusat massa silinder. Menurut hukum Newton:
a. Persamaan gerak dalam arah normal adalah N – mg cos Θ = 0.
b. Persamaan gerak sepanjang bidang miring adalah mg sin Θ – f = ma.
c. Gerak rotasi terhadap pusat massanya τ= I x α .
Gaya normal N dan gaya berat mg tidak dapat menimbulkan rotasi
terhadap titik O. Hal ini disebabkan garis kerja gaya melalui titik O, sehingga lengan momennya sama dengan nol. Persamaan yang berlaku adalah sebagai berikut.
sedangkan untuk rumus kecepatan benda di dasar bidang miring setelah menggelinding adalah sebagai berikut.

Contoh 1, menghitung percepatan bola pada bidang miring

Sebuah benda pejal bermassa M dan berjari-jari R, memiliki momen inersia I = kMR². Benda tersebut menggelinding pada suatu bidang miring dengan sudut kemiringan, seperti tampak pada gambar.
a. Berapakah percepatan yang dialami benda pejal tersebut?
b. Tentukanlah percepatan yang terjadi, jika benda itu berupa bola dengan momen inersia I =(2/5)MR², atau silinder dengan I = ½ MR².

Jawab
Diketahui: I benda pejal = kMR².

a. Menurut Hukum Kedua Newton pada gerak translasi, diperoleh hubungan

Mg sin θ – f = Ma atau Ma + f = Mg sin θ …. (a)

Berdasarkan prinsip rotasi terhadap pusat benda, berlaku hubungan

τ = Iα → f R = kMR α→ f = kMa …. (b)

Substitusikan Persamaan (b) ke dalam Persamaan (a), diperoleh

Ma + kMa = Mg sinθ ⇨ a = (g sinθ) / (k +1)

b. Untuk silinder dengan k = ½ , diperoleh

a = (g sinθ) / ( ½ + 1) = (2/3) (g sinθ)

Contoh 2 :

Sebuah silinder pejal bermassa M dan berjari-jari R diletakkan pada bidang miring dengan kemiringan θ terhadap bidang horisontal yang mempunyai kekasaran tertentu. Setelah dilepas silinder tersebut menggelinding, tentukan kecepatan silinder setelah sampai di kaki bidang miring!

Cara penyelesaiannya:

Persoalan ini dapat diselesaikan menggunakan konsep dinamika atau menggunakan hukum kekekalan tenaga mekanik.

a. Penyelesaian secara dinamika

Silinder menggelinding karena bidang miring mempunyai tingkat kekasaran tertentu. Momen gaya terhadap sumbu putar yang menyebabkan silinder berotasi dengan percepatan sudut α ditimbulkan oleh gaya gesek f, yang dapat ditentukan melalui fR = Iα

Karena momen inersia silinder terhadap sumbunya adalah I =1/2MR² dan percepatan linier a = αR, maka gaya gesek dapat dinyatakan sebagai f = ½ Ma

Pada gerak menggelinding tersebut pusat massa silinder bergerak translasi, sehingga berlaku hukum kedua Newton.

Mg sin θ – f = Ma

Setelah memasukkan harga f di atas dapat diketahui percepatan linier silinder, yaitu a = 2/3 g Sinθ

Dengan menggunakan hubungan v²= v_o²+ 2as, dan mengingat kecepatan silinder saat terlepas v_o = 0 dan h = s sin θ, maka

kecepatan silinder setelah sampai di ujung kaki bidang adalah:

V² = 4/3 gh

Terlihat bahwa kecepatan benda menggelinding lebih lambat daripada bila benda tersebut tergelincir (meluncur) tanpa gesekan yang kecepatannya:

V²= 2gh

b. Penyelesaian menggunakan kekekalan tenaga mekanik

Pada gerak menggelinding berlaku hukum kekekalan tenaga mekanik, tenaga mekanik silinder pada kedudukan 1 adalah:

E_I = Ep_I = Mg (h + R)

Sedangkan tenaga mekanik silinder pada kedudukan 2 adalah:

E₂ = Ep₂ + Ek₂+ EkR₂
mgR + 1/2 mv² + 1/2 Iω²

Perubahan tenaga mekanik yang terjadi adalah

W_f= ΔE = E₂– E₁ = ½ Mv ² + 1/2 Iω² − Mgh

Karena Wf = 0, maka dengan memasukkan momen inersia silinder I =1/2MR²

ϖ = v/R , kecepatan silinder setelah sampai di ujung kaki bidang miring besarnya adalah:

V² = 4/3 gh

3. APLIKASI HUKUM KEKEKALAN MOMENTUM SUDUT

Hukum Kekekalan Momentum Sudut
Bila momen gaya eksternal resultan yang bekerja pada suatu benda tegar sama dengan nol, maka momentum sudut total sistem tetap. Prinsip ini dikenal sebagai prinsip kekekalan momentum sudut.

Jika benda tegar berotasi dengan dua keadaan momentum sudut yang berbeda, maka hukum kekekalan momentum sudut dapat dituliskan sebagai
I₁ω₁=I₂ω₂

Beberapa aplikasi hukum kekekalan momentum sudut

a. Penari balet
seorang penari balet akan menarik tangannya ke dekat badannya untuk berputar lebih cepat dan mengembangkan kedua tangannya untuk berputar lebih lambat. Ketika penari balet menarik kedua tangannya ke dekat badannya, momen inersia sistem berkurang sehingga kecepatan sudut penari balet semakin besar. Sebaliknya, ketika kedua tangan mengembang momen inersia sistem meningkat sehingga kecepatan sudut penari balet semakin kecil

b. Pelompat indah
Pada saat pelompat indah hendak melakukan putaran di udara, ia akan menekuk tubuhnya. hal ini akan mengurangi momen inersianya sehingga kecepatan sudutnya semakin besar, menyebabkan pelompat indah dapat berputar satu setengah putaran

Sumber : yiksrimustika dan budisma dan fisika79