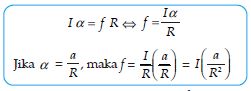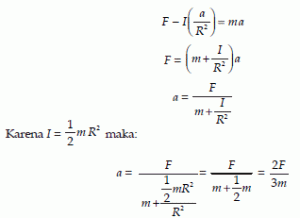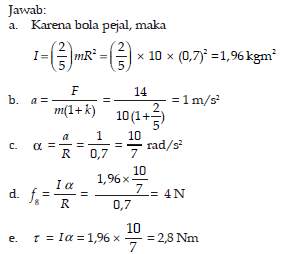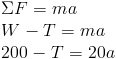Kesetimbangan adalah suatu kondisi benda dengan resultan gaya dan resultan momen gaya sama dengan nol.
Kesetimbangan biasa terjadi pada :
Kesetimbangan benda tegar dibedakan menjadi dua:
A. Keseimbangan Partikel
Partikel adalah benda yang ukurannya dapat diabaikan dan hanya mengalami gerak translasi (tidak mengalami gerak rotasi).
Syarat kesetimbangan partikel SF = 0 à SFx = 0 (sumbu X)
SFy = 0 (sumbu Y)
B. Keseimbangan Benda
Jika benda dipengaruhi gaya yang jumlahnya nol ΣF = 0 maka benda akan lembam atau seimbang translasi. Hukum I Newton dapat dikembangkan untuk gerak rotasi. Jika suatu benda dipengaruhi momen gaya yang jumlahnya nol (Στ = 0) maka benda tersebut akan seimbang rotasi.
Kedua syarat di atas itulah yang dapat digunakan untuk menjelaskan mengapa sebuah benda tegar itu seimbang. Sebuah benda tegar akan seimbang jika memenuhi keadaan syarat di atas. Berarti berlaku syarat di bawah.

Soal dan Penyelesaian

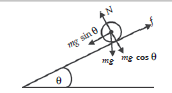
1.Sebuah papan panjangnya 2 m diberi penopang tiap-tiap ujungnya seperti pada Gambar. Massa papan 10 kg. Pada jarak 50 cm dari penopang B diletakkan beban 80 N. Jika sistem dalam keadaan seimbang maka tentukan gaya tekan normal yang bekerja di titik A dan B!
Penyelesaian :
Untuk menentukan nilai NA dan NB dapat digunakan syarat persamaan di atas. Karena keduanya belum diketahui, gunakan syarat Στ = 0 terlebih dahulu.
Acuan titik A
Momen gaya yang bekerja dari titik A dapat digambarkan seperti pada Gambar , dan
berlaku syarat berikut.
ΣτA = 0
(AB). NB − (AO). wAB − (AC) . w = 0
2 . NB − 1. 100 − 1,5 . 80 = 0
2 NB = 220
NB = 110 N
Nilai NA dapat ditentukan dengan syarat ΣF = 0 sehingga diperoleh :
ΣF = 0
NA + NB − wAB − w = 0
NA + 110 − 100 − 80 = 0
NA = 70 N
2. Sebuah papan nama bermassa 10 kg digantung pada batang bermassa 4 kg seperti pada Gambar (a). Agar sistem dalam keadaan seimbang maka berapakah tegangan minimum yang dapat ditarik oleh tali BC?

Penyelesaian :
Tegangan T minimum adalah besar tegangan yang dapat menyebabkan sistem itu seimbang sesuai beratnya. Gaya dan momen gayanya dapat
digambarkan seperti pada Gambar (b).
Nilai T dapat ditentukan dengan syarat Στ = 0 di titik A.
ΣτA = 0
(AB).T sin 30O− (AB).wAB−(AB).w = 0
l . T . − l . 40 − l . 100 = 0
T − 40 − 200 = 0
T = 240 N
3. Sebuah roda mamiliki massa 13 kg dan jari – jari 1 m. bertumpu dilantai dan bersandar pada anak tangga yang tingginya 0,6 m dari lantai seperti pada gambar. Tentukan gaya mendatar F minimum untuk mengungkit roda jika g = 10 m/s2!
R = 1m
h = 0,6 m
ditanyakan : F min…..?
jawab : W = m .g
= 13.10
= 130 N
l1 = R- h
= 1 – 0,6
= 0,4
l2 = Ö(R2 – l12)
= Ö(12 – 0,42)
= Ö(1 – 0,16)
= Ö0,84
tS = 0
t1 + t2 = 0
F . l1 – W . l2 = 0
F . 0,4 – 130 . Ö0,84 = 0
F = (130Ö0,84)/0,4
= 325Ö0,84 N
4. Suatu batang pemikul AB panjangnya 90 cm (berat diabaikan) dipakai untuk memikul beban A dan B masing – masing beratnya 48 N dan 42 N. supaya batang setimbang, orang harus memikul (menumpu) di C. maka tentukan jarak AC!
FA = 48 N
FB = 48 N
Ditanyakan : Jarak AC…?
Jawaban : misal jarak AC adalah x maka BC adalah 90 – x
tS = 0
tA + tB = 0
-WA . lA + WB . lB = 0
-48x + 42 (90 – x) = 0
-48x + 3780 – 42x = 0
-90x = 3780
x = 3780/90 = 42 cm
Sumber : Fisika-Ceria dan Dewi
Baca Selengkapnya
Kesetimbangan biasa terjadi pada :
- Benda yang diam (statik), contoh : semua bangunan gedung, jembatan, pelabuhan, dan lain-lain.
- Benda yang bergerak lurus beraturan (dinamik), contoh : gerak meteor di ruang hampa, gerak kereta api di luar kota, elektron mengelilingi inti atom, dan lain-lain.
Kesetimbangan benda tegar dibedakan menjadi dua:
- Kesetimbangan partikel
- Kesetimbangan benda
A. Keseimbangan Partikel
Partikel adalah benda yang ukurannya dapat diabaikan dan hanya mengalami gerak translasi (tidak mengalami gerak rotasi).
Syarat kesetimbangan partikel SF = 0 à SFx = 0 (sumbu X)
SFy = 0 (sumbu Y)
B. Keseimbangan Benda
Jika benda dipengaruhi gaya yang jumlahnya nol ΣF = 0 maka benda akan lembam atau seimbang translasi. Hukum I Newton dapat dikembangkan untuk gerak rotasi. Jika suatu benda dipengaruhi momen gaya yang jumlahnya nol (Στ = 0) maka benda tersebut akan seimbang rotasi.
Kedua syarat di atas itulah yang dapat digunakan untuk menjelaskan mengapa sebuah benda tegar itu seimbang. Sebuah benda tegar akan seimbang jika memenuhi keadaan syarat di atas. Berarti berlaku syarat di bawah.

Soal dan Penyelesaian

1.Sebuah papan panjangnya 2 m diberi penopang tiap-tiap ujungnya seperti pada Gambar. Massa papan 10 kg. Pada jarak 50 cm dari penopang B diletakkan beban 80 N. Jika sistem dalam keadaan seimbang maka tentukan gaya tekan normal yang bekerja di titik A dan B!
Penyelesaian :
Untuk menentukan nilai NA dan NB dapat digunakan syarat persamaan di atas. Karena keduanya belum diketahui, gunakan syarat Στ = 0 terlebih dahulu.
Acuan titik A
Momen gaya yang bekerja dari titik A dapat digambarkan seperti pada Gambar , dan
berlaku syarat berikut.
ΣτA = 0
(AB). NB − (AO). wAB − (AC) . w = 0
2 . NB − 1. 100 − 1,5 . 80 = 0
2 NB = 220
NB = 110 N
Nilai NA dapat ditentukan dengan syarat ΣF = 0 sehingga diperoleh :
ΣF = 0
NA + NB − wAB − w = 0
NA + 110 − 100 − 80 = 0
NA = 70 N
2. Sebuah papan nama bermassa 10 kg digantung pada batang bermassa 4 kg seperti pada Gambar (a). Agar sistem dalam keadaan seimbang maka berapakah tegangan minimum yang dapat ditarik oleh tali BC?

Penyelesaian :
Tegangan T minimum adalah besar tegangan yang dapat menyebabkan sistem itu seimbang sesuai beratnya. Gaya dan momen gayanya dapat
digambarkan seperti pada Gambar (b).
Nilai T dapat ditentukan dengan syarat Στ = 0 di titik A.
ΣτA = 0
(AB).T sin 30O− (AB).wAB−(AB).w = 0
l . T . − l . 40 − l . 100 = 0
T − 40 − 200 = 0
T = 240 N
3. Sebuah roda mamiliki massa 13 kg dan jari – jari 1 m. bertumpu dilantai dan bersandar pada anak tangga yang tingginya 0,6 m dari lantai seperti pada gambar. Tentukan gaya mendatar F minimum untuk mengungkit roda jika g = 10 m/s2!
R = 1m
h = 0,6 m
ditanyakan : F min…..?
jawab : W = m .g
= 13.10
= 130 N
l1 = R- h
= 1 – 0,6
= 0,4
l2 = Ö(R2 – l12)
= Ö(12 – 0,42)
= Ö(1 – 0,16)
= Ö0,84
tS = 0
t1 + t2 = 0
F . l1 – W . l2 = 0
F . 0,4 – 130 . Ö0,84 = 0
F = (130Ö0,84)/0,4
= 325Ö0,84 N
4. Suatu batang pemikul AB panjangnya 90 cm (berat diabaikan) dipakai untuk memikul beban A dan B masing – masing beratnya 48 N dan 42 N. supaya batang setimbang, orang harus memikul (menumpu) di C. maka tentukan jarak AC!
FA = 48 N
FB = 48 N
Ditanyakan : Jarak AC…?
Jawaban : misal jarak AC adalah x maka BC adalah 90 – x
tS = 0
tA + tB = 0
-WA . lA + WB . lB = 0
-48x + 42 (90 – x) = 0
-48x + 3780 – 42x = 0
-90x = 3780
x = 3780/90 = 42 cm
Sumber : Fisika-Ceria dan Dewi