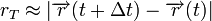Pengertian Gerak Melingkar
Dalam kehidupan sehari-hari sering kita jumpai berbagai macam gerak melingkar, seperti compact disc (CD), gerak bulan mengelilingi bumi, perputaran roda ban mobil atau motor, komidi putar, dan sebagainya.
Jika kita perhatikan benda-benda tersebut pada saat bergerak, maka dikatakan benda melakukan gerak melingkar yang selama pergerakkannya berada dalam bidang datar.
Gerak Melingkar adalah gerak benda pada lintasan yang berbentuk lingkaran. Gerak melingkar sama halnya dengan gerak lurus dibagi menjadi dua : Gerak Melingkar Beraturan (GMB) dan Gerak Melingkar Berubah Beraturan (GMBB).
Gerak melingkar beraturan
Gerak Melingkar Beraturan (GMB) adalah gerak melingkar dengan besar kecepatan sudut

tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial
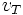
dengan jari-jari lintasan

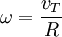
Arah kecepatan linier
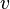
dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial
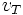
. Tetapnya nilai kecepatan
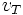
akibat konsekuensi dar tetapnya nilai

. Selain itu terdapat pula percepatan radial

yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.

Bila
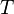
adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran

, maka dapat pula dituliskan

Kinematika gerak melingkar beraturan adalah

dengan

adalah sudut yang dilalui pada suatu saat
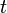
,

adalah sudut mula-mula dan

adalah kecepatan sudut (yang tetap nilainya).
Gerak melingkar berubah beraturan
Gerak Melingkar Berubah Beraturan (GMBB) adalah gerak melingkar dengan percepatan sudut

tetap. Dalam gerak ini terdapat percepatan tangensial

(yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial
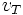
).

Kinematika GMBB adalah



dengan

adalah percepatan sudut yang bernilai tetap dan

adalah kecepatan sudut mula-mula.
Turunan dan integral
Seperti halnya kembarannya dalam gerak linier, besaran-besaran gerak melingkar pun memiliki hubungan satu sama lain melalui proses integrasi dan diferensiasi.

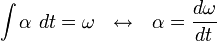
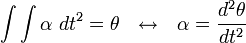
[sunting] Hubungan antar besaran sudut dan tangensial
Antara besaran gerak linier dan melingkar terdapat suatu hubungan melalui

khusus untuk komponen tangensial, yaitu

Perhatikan bahwa di sini digunakan

yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu
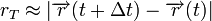
untuk suatu selang waktu kecil atau sudut yang sempit.
Besaran-Besaran Fisis dalam Gerak Melingkar
Dalam gerak lurus mengenal tiga besaran utama yaitu perpindahan (linear), kecepatan (linear) dan Percepatan (linear). Gerak melingkar juga memiliki tiga komponen tersebut, yaitu
perpindahan sudut, kecepatan sudut dan percepatan sudut. Pada gerak lurus juga mengenal
Gerak Lurus Beraturan dan
Gerak Lurus Berubah Beraturan. Dalam gerak melingkar juga terdapat
Gerak Melingkar Beraturan (GMB) dan Gerak Melingkar Berubah Beraturan (GMBB).
Ada tiga cara menghitung sudut.
Cara pertama adalah menghitung sudut dalam derajat (
o). Satu lingkaran penuh sama dengan 360
o.
Cara kedua adalah mengukur sudut dalam putaran. Satu lingkaran penuh sama dengan satu putaran. Dengan demikian, satu putaran = 360
o. Cara ketiga adalah dengan radian. Radian adalah satuan Sistem Internasional (SI) untuk perpindahan sudut, sehingga satuan ini akan sering kita gunakan dalam perhitungan.
*Kecepatan Sudut
Dalam gerak melingkar, bagian yang berbeda memiliki kecepatan yang berbeda. Misalnya gerak roda yang berputar. Bagian roda yang dekat dengan poros bergerak dengan kecepatan linear yang lebih kecil, sedangkan bagian yang jauh dari poros alias pusat roda bergerak dengan kecepatan linear yang lebih besar
Pada gerak melingkar, kelajuan rotasi benda dinyatakan dengan putaran per menit (biasa disingkat rpm – revolution per minute). Kelajuan yang dinyatakan dengan satuan rpm adalah kelajuan sudut. Dalam gerak melingkar, kita juga dapat menyatakan arah putaran. misalnya kita menggunakan arah putaran jarum jam sebagai patokan. Oleh karena itu, kita dapat menyatakan kecepatan sudut, di mana selain menyatakan kelajuan sudut, juga menyatakan arahnya (ingat perbedaan kelajuan dan kecepatan, mengenai hal ini sudah Gurumuda terangkan pada Pokok bahasan Kinematika). Jika kecepatan pada gerak lurus disebut kecepatan linear (benda bergerak pada lintasan lurus), maka kecepatan pada gerak melingkar disebut kecepatan sudut, karena benda bergerak melalui sudut tertentu.
Terdapat dua jenis kecepatan pada Gerak Lurus, yakni kecepatan rata-rata dan kecepatan sesaat. Kita dapat mengetahui kecepatan rata-rata pada Gerak Lurus dengan membandingkan besarnya perpindahan yang ditempuh oleh benda dan waktu yang dibutuhkan benda untuk bergerak . Nah, pada gerak melingkar, kita dapat menghitung kecepatan sudut rata-rata dengan membandingkan perpindahan sudut dengan selang waktu yang dibutuhkan ketika benda berputar. Secara matematis kita tulis :
 Kecepatan sudut sesaat
Kecepatan sudut sesaat kita diperoleh dengan membandingkan
perpindahan sudut dengan
selang waktu yang sangat singkat. Secara matematis kita tulis :

Sesuai dengan kesepakatan ilmiah, jika ditulis kecepatan sudut maka yang dimaksud adalah kecepatan sudut sesaat. Kecepatan sudut termasuk besaran vektor. Vektor kecepatan sudut hanya memiliki dua arah
(searah dengan putaran jarum jam atau berlawanan arah dengan putaran jarum jam), dengan demikian notasi vektor omega dapat ditulis dengan huruf miring dan cukup dengan memberi tanda positif atau negatif. Jika pada Gerak Lurus arah kecepatan sama dengan arah perpindahan, maka pada Gerak Melingkar, arah kecepatan sudut sama dengan arah perpindahan sudut.
*Percepatan Sudut
Dalam gerak melingkar, terdapat percepatan sudut apabila ada perubahan kecepatan sudut. Percepatan sudut terdiri dari percepatan sudut sesaat dan percepatan sudut rata-rata. Percepatan sudut rata-rata diperoleh dengan membandingkan perubahan kecepatan sudut dan selang waktu. Secara matematis ditulis :
Percepatan sudut sesaat diperoleh dengan membandingkan perubahan sudut dengan selang waktu yang sangat singkat. Secara matematis ditulis :

Gerak lurus dan gerak melingkar
Dalam gerak melingkar, arah kecepatan linear dan percepatan linear selalu menyinggung lingkaran. Karenanya, dalam gerak melingkar, kecepatan linear dikenal juga sebagai kecepatan tangensial dan percepatan linear disebut juga sebagai percepatan tangensial.
Hubungan antara Perpindahan Linear dengan Perpindahan sudut
Pada gerak melingkar, apabila sebuah benda berputar terhadap pusat/porosnya maka setiap bagian benda tersebut bergerak dalam suatu lingkaran yang berpusat pada poros tersebut. Misalnya gerakan roda yang berputar atau bumi yang berotasi. Ketika bumi berotasi, kita yang berada di permukaan bumi juga ikut melakukan gerakan melingkar, di mana gerakan kita berpusat pada pusat bumi. Ketika kita berputar terhadap pusat bumi, kita memiliki kecepatan linear, yang arahnya selalu menyinggung lintasan rotasi bumi.
Perhatikanlah gambar di bawah ini.

ketika benda berputar terhadap poros O, titik A memiliki kecepatan linear (
v) yang arahnya selalu menyinggung lintasan lingkaran.
Hubungan antara perpindahan linear titik A yang menempuh lintasan lingkaran sejauh x dan perpindahan sudut teta (dalam satuan radian), dinyatakan sebagai berikut :
Di mana r merupakan jarak titik A ke pusat lingkaran/jari-jari lingkaran.
Hubungan antara Kecepatan Tangensial dengan Kecepatan sudut
Sumber :
Widiaprianto dan
Desiana Putri















.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
.gif)
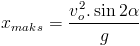.gif)
.gif)
 tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial
tetap. Besar Kecepatan sudut diperolah dengan membagi kecepatan tangensial 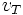 dengan jari-jari lintasan
dengan jari-jari lintasan 
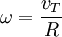
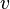 dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial
dalam GMB selalu menyinggung lintasan, yang berarti arahnya sama dengan arah kecepatan tangensial  yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
yang besarnya tetap dengan arah yang berubah. Percepatan ini disebut sebagai percepatan sentripetal, di mana arahnya selalu menunjuk ke pusat lingkaran.
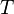 adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran
adalah waktu yang dibutuhkan untuk menyelesaikan satu putaran penuh dalam lintasan lingkaran  , maka dapat pula dituliskan
, maka dapat pula dituliskan

 adalah sudut yang dilalui pada suatu saat
adalah sudut yang dilalui pada suatu saat 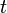 ,
,  adalah sudut mula-mula dan
adalah sudut mula-mula dan  tetap. Dalam gerak ini terdapat percepatan tangensial
tetap. Dalam gerak ini terdapat percepatan tangensial  (yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial
(yang dalam hal ini sama dengan percepatan linier) yang menyinggung lintasan lingkaran (berhimpit dengan arah kecepatan tangensial 



 adalah kecepatan sudut mula-mula.
adalah kecepatan sudut mula-mula.
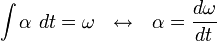
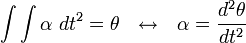

 yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu
yang didefinisikan sebagai jarak yang ditempuh atau tali busur yang telah dilewati dalam suatu selang waktu dan bukan hanya posisi pada suatu saat, yaitu